Дана трапеция ABCD, основания которой BC = 44, AD = 100, AB = CD = 35. Окружность, касающаяся прямых AD и AC, касается стороны CD в точке K. Найдите длину отрезка CK.
Найдем диагональ AC. Опустим из вершин B и С на сторону AD перпендикуляры BE и СF соответственно. AE = FD, так как трапеция равнобедренная. BCFE — прямоугольник.
Возможны две геометрические конфигурации.
Первый вариант: окружность вписана в треугольник ACD:
Второй вариант: окружность касается продолжения сторон AC и AD за точками C и D соответственно и отрезка CD:
Ответ: 5 или 30.
Примечание.
Решение опирается на известную теорему: расстояние от вершины треугольника до точки касания исходящей из этой вершины стороны со вписанной в треугольник окружностью, равно разности полупериметра треугольника и стороны, противолежащей этой вершине.
Прошу прощения, но вторая часть решения, где "СК= ..." вызывает вопросы. Нужно вначале доказать, что ADC прямоугольный, чтобы воспользоваться формулой радиуса вписаной в него окружности. В этом случае, СК - сторона квадрата и равна радиусу.
Но ничего этого в решении нет, кроме того, ADC не прямоугольный, что доказывается по теореме Пифагора.
В чем же секрет вашего решения?
Откуда взята формула "СК=..." (хотя бы в первом случае) ?
Спасибо заранее.
Секрет решения прост.
Отрезки касательных, проведенных из одной точки, равны.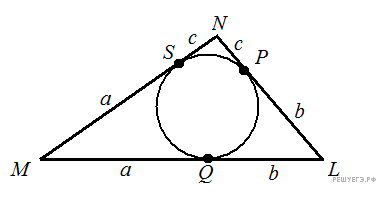
Для любого треугольника, в который вписана окружность верно:
Для
проверьте сами...
Здравствуйте. Во второй случае, когда мы ищем СК, непонятно, почему СК=... Вы можете привести доказательство. Заранее спасибо.
Все по той же причине равенства отрезков касательных проведенных из одной точки.