Тип Д10 C2 № 509475 

Сложная стереометрия. Круглые тела
i
Боковое ребро правильной четырёхугольной пирамиды равно b, а плоский угол при вершине равен α. Найдите радиус сферы описанной около пирамиды.
Решение. 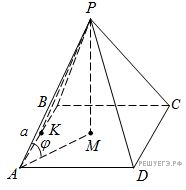
Пусть PABCD — правильная четырёхугольная пирамида с вершиной P, M — центр основания ABCD, K — середина ребра AB. Обозначим AB = a, ∠MAP = φ.
Так как PK — высота равнобедренного треугольника APB, то

Из прямоугольного треугольника AMP находим, что

Тогда

(угол MAP — острый).

Пусть R — искомый радиус. Рассмотрим сечение пирамиды и описанной около неё сферы плоскостью, проходящей через точки A, P и C. Получим равнобедренный треугольник APC, вписанный в окружность радиуса R. По теореме синусов

Ответ: 
Спрятать критерииКритерии проверки:| Критерии оценивания выполнения задания | Баллы |
|---|
| Имеется верное доказательство утверждения пункта а), и обоснованно получен верный ответ в пункте б) | 3 |
| Получен обоснованный ответ в пункте б) ИЛИ имеется верное доказательство утверждения пункта а), и при обоснованном решении пункта б) получен неверный ответ из-за арифметической ошибки | 2 |
| Имеется верное доказательство утверждения пункта а), ИЛИ при обоснованном решении пункта б) получен неверный ответ из-за арифметической ошибки, ИЛИ обоснованно получен верный ответ в пункте б) с использованием утверждения пункта а), при этом пункт а) не выполнен | 1 |
| Решение не соответствует ни одному из критериев, приведённых выше | 0 |
| Максимальный балл | 3 |
Ответ: 



