Тип Д15 C4 № 505873 

Сложная планиметрия. Треугольники
i
Дан треугольник АВС, в котором АС = СВ, а синус угла С равен 1. Треугольник ABD — равнобедренный, с боковой стороной равной 10. Найдите площадь треугольника АВС.
Решение. Синус угла С равен 1, поэтому угол С прямой, а треугольник АВС прямоугольный. По условию этот треугольник равнобедренный, пусть его катеты AC = BC = x. По теореме Пифагора найдем гипотенузe:  Рассмотрим два случая, изображенных на рисунке.
Рассмотрим два случая, изображенных на рисунке.
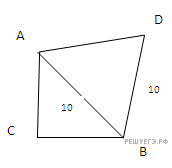

Случай 1: AB = BD = 10. Из равенства  находим
находим  а значит,
а значит, 
Случай 2: AD = BD = 10. В силу неравенства треугольника имеем:  то есть
то есть

Следовательно,  Заметим, что второй случай включает в себя первый.
Заметим, что второй случай включает в себя первый.
Ответ: любое число, принадлежащее интервалу (0; 100).
Спрятать критерииКритерии проверки:| Критерии оценивания выполнения задания | Баллы |
|---|
| Имеется верное доказательство утверждения пункта а и обоснованно получен верный ответ в пункте б. | 3 |
| Получен обоснованный ответ в пункте б. ИЛИ Имеется верное доказательство утверждения пункта а и при обоснованном решении пункта б получен неверный ответ из-за арифметической ошибки. | 2 |
| Имеется верное доказательство утверждения пункта а. ИЛИ При обоснованном решении пункта б получен неверный ответ из-за арифметической ошибки. ИЛИ Обоснованно получен верный ответ в пункте б и использованием утверждения пункта а, при этом пункт а не выполнен. | 1 |
| Решение не соответствует ни одному из критериев, перечисленных выше. | 0 |
| Максимальный балл | 3 |
Ответ: любое число, принадлежащее интервалу (0; 100).
Рассмотрим два случая, изображенных на рисунке.
находим
а значит,
то есть
Заметим, что второй случай включает в себя первый.




Здравствуйте. Под модулем во втором случае есть опечатка: пропущена буква А.
Переписали решение. Спасибо за ваши комментарии!