Плоскость α пересекает два шара, имеющих общий центр. Площадь сечения меньшего шара этой плоскостью равна 8. Плоскость β, параллельная плоскости α, касается меньшего шара, а площадь сечения этой плоскостью большего шара равна 5.
а) Докажите, что сечение шара плоскостью α есть круг.
б) Найдите площадь сечения большего шара плоскостью α.
а) Пусть α — секущая плоскость и О — центр шара. Опустим перпендикуляр из центра шара на плоскость α и обозначим через F основание этого перпендикуляра.
Пусть X — произвольная точка шара, принадлежащая плоскости α. По теореме Пифагора ОХ не больше радиуса R шара, поэтому
то есть любая точка сечения шара плоскостью α находится от точки F на расстоянии, не большем
следовательно, она принадлежит шару. Это значит, что любая точка сечения шара плоскостью α лежит в круге с центром в точке F.
Обратно: любая точка X этого круга принадлежит шару и лежит в плоскости α, а это значит, что сечение шара плоскостью α есть круг с центром в точке F.
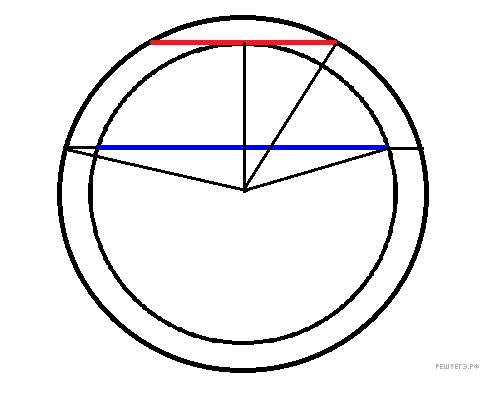
б) Рассмотрим сечение, проходящее через общий центр шаров и центры сечений — кругов. Обозначение центра, точки касания и точек пересечения поверхностей шаров с плоскостями
FD — радиус круга, полученного в сечении меньшего шара плоскостью α, тогда — площадь сечения меньшего шара плоскостью α.
AB — радиус круга, полученного в сечении большего шара плоскостью β, тогда — площадь сечения большего шара плоскостью β.
CF — радиус круга, полученного в сечении большего шара плоскостью α.
Параллельные прямые AB и CF перпендикулярны прямой AF. Из прямоугольных треугольников получаем:
откуда
Площадь сечения большего шара плоскостью α:
Ответ: б) 13.




Из решения следует, что AB=(5/pi)^1/2 и FD=(8/pi)^1/2. Значит АB<FD. Но даже на рисунке видно, что AB>FD. И вообще, не понятно, как может площадь сечения МЕНЬШЕГО шара (=8 по условию) может быть больше, чем площадь сечения БОЛЬШЕГО шара (=5 по условию), касательная к меньшему шару.
А такой рисунок примирит Вас с условием задачи?