Тип 17 № 511395 

Планиметрическая задача. Вписанные окружности и треугольники
i
Дан равнобедренный треугольник ABC с основанием AC. Вписанная в него окружность с центром O касается боковой стороны BC в точке P и пересекает биссектрису угла B в точке Q.
а) Докажите, что отрезки PQ и OC параллельны.
б) Найдите площадь треугольника OBC, если точка O делит высоту BD треугольника в отношении BO : OD = 3 : 1 и AC = 2.
Решение. 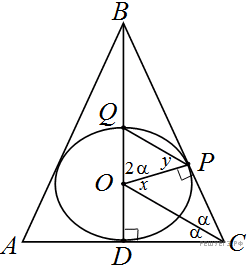
Пусть отрезок BD — высота данного треугольника. Тогда  в силу того, что ABC — равнобедренный треугольник. Введем следующие обозначения:
в силу того, что ABC — равнобедренный треугольник. Введем следующие обозначения: 

 Прямоугольные треугольники BOP и BCD подобны, следовательно,
Прямоугольные треугольники BOP и BCD подобны, следовательно,  Из прямоугольного треугольника OPC находим
Из прямоугольного треугольника OPC находим  а из равнобедренного треугольника OPQ находим
а из равнобедренного треугольника OPQ находим  Углы COP и OPQ ― накрест лежащие при пересечении прямых PQ и OC секущей OP, значит, отрезки PQ и OC параллельны, что и требовалось доказать.
Углы COP и OPQ ― накрест лежащие при пересечении прямых PQ и OC секущей OP, значит, отрезки PQ и OC параллельны, что и требовалось доказать.
б) Отрезок CO ― биссектриса треугольника BCD, следовательно:

Откуда 
 значит,
значит,  и, следовательно:
и, следовательно:

Откуда  По формуле Герона находим:
По формуле Герона находим:

откуда 
Ответ: 
Приведем решение пункта б) Ларисы Максименко.
Отрезок CO ― биссектриса треугольника BCD, следовательно:

откуда  Тогда
Тогда

а значит, 
Найдем площадь треугольника BOC как разность площадей треугольников BDC и ODC:

Критерии проверки:| Критерии оценивания выполнения задания | Баллы |
|---|
| Имеется верное доказательство утверждения пункта a) и обоснованно получен верный ответ в пункте б) | 3 |
| Получен обоснованный ответ в пункте б) ИЛИ имеется верное доказательство утверждения пункта а) и при обоснованном решении пункта б) получен неверный ответ из-за арифметической ошибки | 2 |
| Имеется верное доказательство утверждения пункта а) ИЛИ при обоснованном решении пункта б) получен неверный ответ из-за арифметической ошибки, ИЛИ обоснованно получен верный ответ в пункте б) с использованием утверждения пункта а), при этом пункт а) не выполнен | 1 |
| Решение не соответствует ни одному из критериев, приведённых выше | 0 |
| Максимальный балл | 3 |



