Каталог заданий.
Неравенства с параметром
Неравенства с параметром
Пройти тестирование по этим заданиям
Вернуться к каталогу заданий
Версия для печати и копирования в MS Word
1
Найти все значения параметра a, при каждом из которых неравенство выполняется для всех x.
Оно, очевидно, достигается при 
то есть при 
поскольку 
и оба равенства достигаются в указанных точках.
2
Найти все значения параметра p, при каждом из которых множество решений неравенства 
не содержит ни одного решения неравенства 
и 
(рис. 1). Для этого построим график уравнения 
— параболу. Эта парабола делит плоскость на две области. Соотношению 
Далее, построим график уравнения 
— прямую, которая разбивает плоскость на две полуплоскости. Соотношению 
Выделим общие точки (пересечение) найденных областей (см. рис. 1).
и 
(см. рис. 2). 
Одновременно исключим из полученных результатов полосу, задаваемую неравенством 
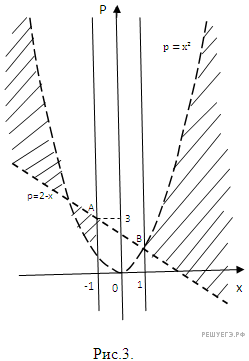
т. е. соотношением 
(см. рис. 3).
и 
прямых 
и 
справа — прямой 
сверху — прямой 
все граничные точки не включены. Каждая точка, принадлежащая указанной фигуре, имеет ординату, принадлежащую интервалу (0; 3). Следовательно, искомые значения параметра p заполнят весь промежуток 
3
Найти все значения параметра а, при которых неравенство 
выполняется для всех х, таких, что 
достаточно выполнения условия: 
4
Найдите все значения х, удовлетворяющие неравенству 
хотя бы при одном значении а, принадлежащем отрезку [-2; 1].
Этот квадратный трехчлен относительно а будет неположительным, если одновременно будут выполняться условия: 
и 
5
Найти все значения параметра p, для которых неравенство 
выполняется хотя бы для одного числа x такого, что | x | < 0,01.
это невозможно.
то подходит 
так как 
)
Решая неравенство методом интервалов, получим 
Учитывая ОДЗ, получим 
Решая неравенство методом интервалов, получим 
Учитывая ОДЗ, получим 
Нужные точки найдутся в этом множестве если 
Пройти тестирование по этим заданиям