Тип 3 № 25725 
Стереометрия. Площадь поверхности составного многогранника
i
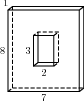
Найдите площадь поверхности многогранника, изображенного на рисунке (все двугранные углы прямые).
Решение.
Это задание ещё не решено, приводим решение прототипа.

Найдите площадь поверхности многогранника, изображенного на рисунке (все двугранные углы прямые).
Площадь поверхности заданного многогранника равна сумме площадей большого и маленького параллелепипедов с ребрами 1, 5, 7 и 1, 1, 2, уменьшенной на 4 площади прямоугольника со сторонами 1, 2 — передней грани маленького параллелепипеда, излишне учтенной при расчете площадей поверхности параллелепипедов:

Ответ: 96.
Приведем другое решение.
Площадь передней грани параллелепипеда равна площади прямоугольника со сторонами 5 и 7, уменьшенной на площадь прямоугольника со сторонами 1 и 2: 
Площадь боковой грани параллелепипеда равна площади прямоугольника со сторонами 1 и 5: 
Площадь нижней грани параллелепипеда равна площади прямоугольника со сторонами 1 и 7: 
Площадь нижней стенки сквозного отверстия равна площади прямоугольника со сторонами 1 и 2: 
Площадь боковой стенки сквозного отверстия равна площади прямоугольника со сторонами 1 и 1: 
Следовательно, площадь поверхности многогранника равна:

Заметим, что первый способ решения намного короче.
Ответ: 140

